C# - Simplificando a raiz quadrada

Hoje vamos recordar alguns conceitos sobre matemática e  brincar com simplificação de radicais usando a linguagem C#.

Vamos começar relembrando alguns conceitos. Abaixo temos a expressão que representa um único número real x que elevado ao índice b resulta o número a :

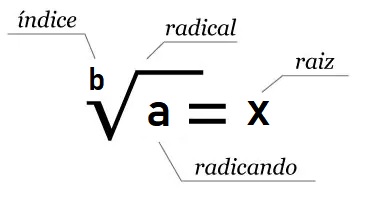A origem do símbolo usado para representar uma raiz é bastante especulativo.

Algumas fontes dizem que o símbolo foi usado pela primeira vez pelos árabes, que o primeiro uso foi de Al-Qalasadi (1421-1486), e que o símbolo vem da letra árabe ?, a primeira letra da palavra "Jadhir".( http://pt.wikipedia.org/wiki/)

Vamos criar um programa na linguagem C# que se propõe a realizar a simplificação da raiz quadrada de qualquer número inteiro.

Abra o Visual C# 2010 Express Edition ou o Visual Studio Community mais recente e no menu File clique em New Project e escolha o template Windows Forms Application informando o nome SimplificarRaizQuadrada;

A seguir inclua no formulário form1.cs os seguintes controles:

Conforme o leiaute abaixo:

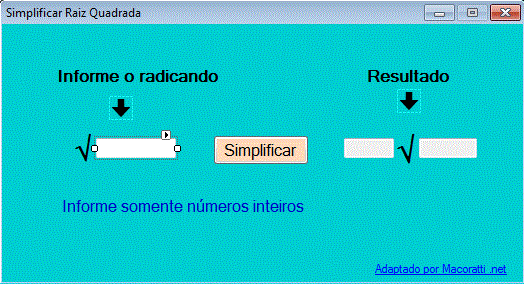No evento Click do botão de comando Simplificar (btnSimplificar) vamos incluir o código abaixo:

       private void btnSimplificar_Click(object sender, EventArgs e)
        {
            //Obtém o valor do radicando informado pelo usuário
            double valorRadicando = double.Parse(txtRadicando.Text);

            //verifica se o numero é um quadrado perfeito
            if (!IsDecimal(Math.Sqrt(valorRadicando)))
            {
                txtResultado1.Text = Math.Sqrt(valorRadicando).ToString();
                txtResultado2.Text = "-";
                return;
            }

            //verifica por inteiros cujo valor do quadrado é um múltiplo do valor informado
            double tQuadrado = 0;
            for (int i = (int)Math.Floor(Math.Sqrt(valorRadicando)); i >= 2; i--)
            {
                tQuadrado = valorRadicando / (double)(i * i);

                if (!IsDecimal(tQuadrado))
                {
                    txtResultado1.Text = i.ToString();
                    txtResultado2.Text = (valorRadicando / (i * i)).ToString();
                    return;
                }
            }

            txtResultado1.Text = "-";
            txtResultado2.Text = "-";
        }

Vamos entender o código...

1- Iniciamos convertendo o valor informado pelo usuário para o radicando para double:

double valorRadicando = double.Parse(txtRadicando.Text);

2- Verificamos a seguir se o número possui um quadrado perfeito. Neste caso apresentamos o resultado:

if (!IsDecimal(Math.Sqrt(valorRadicando)))
{
    txtResultado1.Text = Math.Sqrt(valorRadicando).ToString();
    txtResultado2.Text = "-";
    return;
}

Nota: A função IsDecimal é usada para permitir somente valores inteiros e neste caso verifica se o número obtido é um número inteiro.

private Boolean IsDecimal(double valorRadicando)
 {
            return (int)valorRadicando != valorRadicando;
}

Outro maneira de calcular o quadrado perfeito é obtida usando este código:(No caso para número inteiros)

  public static bool Quadrado_Perfeito(int n)
  {
            if (n < 0)
                return false;

            long tst = (int)(Math.Sqrt(n) + 0.5);
            return tst * tst == n;
     }

3- Iniciamos com o valor inteiro da raiz quadrada do número iniciamos o loop :

for (int i = (int)Math.Floor(Math.Sqrt(valorRadicando)); i >= 2; i--){}

A seguir testamos cada número para ver se ele é um múltiplo do número original. Se for, então você calculamos a raiz quadrada do mesmo e deixamos o restante no interior do sinal de raiz quadrada.

for (int i = (int)Math.Floor(Math.Sqrt(valorRadicando)); i >= 2; i--)
{
   tQuadrado = valorRadicando / (double)(i * i);

  if (!IsDecimal(tQuadrado))
  {
   txtResultado1.Text = i.ToString();
   txtResultado2.Text = (valorRadicando / (i * i)).ToString();
   return;
  }
}

Executando o projeto e realizando um cálculo como exemplo obtemos seguinte resultado:

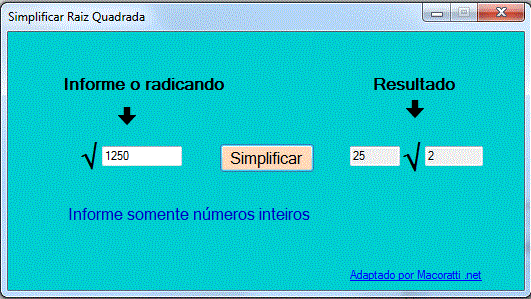O algoritmo usado não é necessariamente o mais otimizado nem esta sujeito a falhas, visto que eu não realizei testes mais apurados. Se você encontrar um algoritmo melhor ou encontrar erros me avise.

Pegue o projeto completo aqui: SimplificarRaiz.zip e  QuadradosPerfeitos.zip

João 14:27 Deixo-vos a paz, a minha paz vos dou; eu não vo-la dou como o mundo a dá. Não se turbe o vosso coração, nem se atemorize.
 

Referências:

José Carlos Macoratti