![]() VB -
Resolução de Sistemas de Equações Lineares
VB -
Resolução de Sistemas de Equações Lineares
Consideramos um sistema de m equações lineares a n incógnitas
com coeficientes reais, escrita sob forma matricial como Ax = b , e
resolver o sistema significa discutir a existência de soluções e obter o
conjunto solução quando for possível . Um dos métodos eficientes mais utilizados
para isso é o Método da Eliminação de Gauss .
O método de eliminação de Gauss
O método consiste em transformar o sistema
linear original para se obter um sistema linear equivalente com mesmo conjunto
solução , usando o método do escalonamento . Podem ser efetuadas as seguintes
operações que não alteram o conjunto solução dos sistemas :
( i ) trocar as posições de
duas equações ;
( i i ) multiplicar uma equação por uma constante não nula ;
( i i i ) adicionar um múltiplo não nulo de uma equação a uma outra equação ;
Efetuam-se as operações acima até obter a
forma escalonada do sistema, A' x = b' , equivalente ao sistema original A x =
b.
Exemplo: Resolver o sistema abaixo com 3 variáveis:
| 3x + 2y - z =
4 4x - y + z = 4 x + y + z = 3 |
Basta trocar somente os elementos das matrizes A e B, e aplicar o método de eliminação de Gauss. |
Aplicando a regra temos:
| A B |
Solução |
||||||||||||
|
x = 1 |
Usando o programa em VB para os valores acima obtemos:
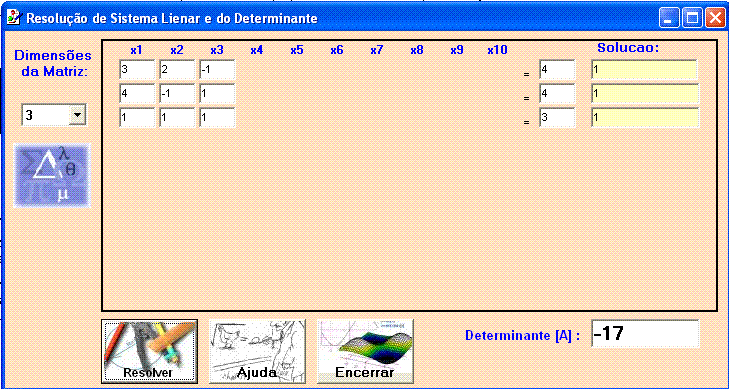
Abaixo temos a tela principal do programa feito em VB que implementa esta solução. A interface gráfica permite trabalhar com uma matriz de 10x10 mas o algoritmo funciona em qualquer situação. O autor do programa não é conhecido. Eu apenas fiz alguns ajustes.
 |
Faça o teste com o seguinte sistema de equações : (Se quiser pode calcular manualmente...)
|
3x + 2y - z +
w = 10 |
O resultado deverá ser
igual a : |
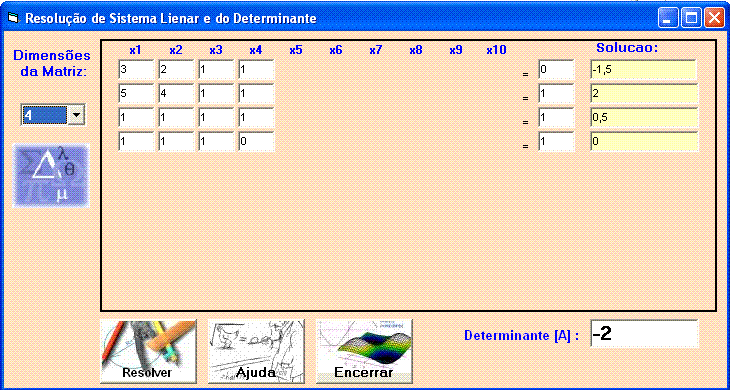
Tente obter o resultado também para o seguinte sistema:
| Sistema com 5 variáveis | Resultado deverá ser igual a: |
| 3x1 + 2x2 -
x3 + x4 + x5 = 10 5x1 + 7x2 - 8x3 + 5x4 + 3x5 = 17 7x1 + 13x2 - 4x3 + 11x4 + 13x5 = 45 x1 + 2x2 + x3 - 17x4 - x5 = 57 4x1 + 15x2 + 5x3 - 19x4 + 2x5 = 89 |
x1 = 2,46167967 x2 = 0,57285452 x3 = -0,626319413 x4 = -3,428866453 x5 = 4,27179899 |
O programa consiste de um módulo contendo as definições para as variáveis globais usadas no projeto:
'Define as variáveis globais Global Dimensao_Sistema_Linear As Integer 'Dimensão do sistema linear Global Matriz_A(1 To 10, 1 To 10) 'Dimensão Máxima da matrix 10x10 para a interface implementada Global Triangular_A(1 To 10, 1 To 11) 'A matriz triangularizada A Global Array_B(10) 'Array de constantes, {B}
Global Solucoes(10) 'Array de soluções {x}
Global Solucao_Problema As Boolean 'Determine se o sistema pode ser resolvido ou não
|
O código completo e comentado do programa é dado a seguir:
Private Sub Command1_Click() frmAJuda.Show vbModal End Sub Private Sub Command2_Click() If (MsgBox("Deseja realmente encerrar o programa ?", vbYesNo, "Encerrar")) = vbYes Then
Unload Me End If End Sub Private Sub Form_Load() 'Atribui numeros de 1 a 10 ao combobox For n = 1 To 10 cboDimensao.AddItem n Next n 'A dimensão padrão é um sistema 2 x 2 cboDimensao.Text = 2 Call Esconde_TextBoxes End Sub 'Resolver um sistema de equacao lineares do tipo [A]{x}={b} para {x}
'e calcula o determinando da matriz [A] Private Sub cmdResolveEquacao_Click() Call Cria_Matrizes Call Cria_Matriz_Triangular Call Retorna_Substituicao End Sub Private Sub cboDimensao_Click() Call Esconde_TextBoxes End Sub Sub Esconde_TextBoxes() Dim n As Integer Dimensao_Sistema_Linear = Val(cboDimensao.Text) 'Dimensao da Matrix [A] 'esconde todos os textboxes : Existem 120 textboxes no formulário de text1(0) a text1(119) 'de 0-99 para a matrix [A] 'de 100-109 para o array de constantes {b}
'de 110-119 para o array de soluções {x}
For n = 0 To 119 ' Text1(n).Visible = False Next n 'esconde as etiquetas com '=' => label2(0) a label2(9) For n = 0 To 9 Label2(n).Visible = False Next n 'Exibe os TextBoexes para a dimensão do sistema escolhido For n = 0 To Dimensao_Sistema_Linear - 1 Label2(n).Visible = True '= Text1(100 + n).Visible = True 'array de constantes {b}
Text1(110 + n).Visible = True 'array de soluções {x}
For k = 0 To 10 * (Dimensao_Sistema_Linear - 1) Step 10 Text1(n + k).Visible = True 'matriz [A] Next k Next n End Sub Sub Cria_Matrizes() 'Cria as matrizes [A] e {B} do sistema linear [A]*{x}={B}
'atribuindo valores a partir dos TextBoxes 'Foi implementado uma matriz de dimensão máxima de 10x10 mas pode ser aumentado 'cria Matriz_A For n = 1 To Dimensao_Sistema_Linear For m = 1 To Dimensao_Sistema_Linear Matriz_A(n, m) = Val(Text1(m - 1 + (n - 1) * 10)) Next m Next n 'Cria o array_B (constantes) For n = 1 To Dimensao_Sistema_Linear Array_B(n) = Val(Text1(99 + n)) Next n End Sub Sub Cria_Matriz_Triangular() ' Usa o método de eliminação de Gauss a fim de criar a matrix triangular a partir da matriz [A] ' A matrix triangularizada Triangular_A é (Dimensao_Sistema_Linear X Dimensao_Sistema_Linear+1) ' pois inclui também o array {b} de constantes
'[ a11 a12 a13 | b1 ] '[ a21 a22 a23 | b2 ] '[ a31 a32 a33 | b3 ] etc 'Se o sistema não puder ser resolvido => (Determinant = 0) On Error GoTo trataErro Solucao_Problema = False 'Atribui valores a partir da matriz [A] For n = 1 To 10 For m = 1 To 10 Triangular_A(m, n) = Matriz_A(m, n) Next Next 'Atribui valores a partir do array {b}
For n = 1 To Dimensao_Sistema_Linear Triangular_A(n, Dimensao_Sistema_Linear + 1) = Array_B(n) Next n 'Triangulariza a matriz For k = 1 To Dimensao_Sistema_Linear - 1 If Triangular_A(k, k) = 0 Then For n = k To Dimensao_Sistema_Linear If Triangular_A(n, k) <> 0 Then line_1 = n Exit For 'encontra o elemento line_1 diferente de zero Next n 'muda a linha k com line_1 For m = k To Dimensao_Sistema_Linear temporary_1 = Triangular_A(k, m) Triangular_A(k, m) = Triangular_A(line_1, m) Triangular_A(line_1, m) = temporary_1 Next m End If 'Para outras linhas, atribui elemento zero usando: 'Ai1=Aij-A11*(Aij/A11) 'e alterando toda a linha usando a mesma formula para os outros elementos For n = k + 1 To Dimensao_Sistema_Linear If Triangular_A(n, k) <> 0 Then 'se for zero deixa estar multiplier_1 = Triangular_A(n, k) / Triangular_A(k, k) For m = k To Dimensao_Sistema_Linear + 1 Triangular_A(n, m) = Triangular_A(n, m) - Triangular_A(k, m) * multiplier_1 Next m End If Next n Next k Exit Sub trataErro: Dim mensagem As String Dim resposta As String mensagem = "Ocorreu um erro durante a solução do processo." & vbCrLf & "Verifique se o sistema pode ser resolvido." resposta = MsgBox(mensagem, vbCritical) Solucao_Problema = True End Sub Sub Retorna_Substituicao() On Error GoTo trataErro 'Calcula o array {x} solução usando a substituição
If Solucao_Problema = True Then Exit Sub
'Primeiro , calcula o último xi (para i=Dimensao_Sistema_Linear)
Solucoes(Dimensao_Sistema_Linear) = Triangular_A(Dimensao_Sistema_Linear, Dimensao_Sistema_Linear + 1) /_
Triangular_A(Dimensao_Sistema_Linear, Dimensao_Sistema_Linear)
'substibuicao para o outro xi:
For n = 1 To Dimensao_Sistema_Linear - 1 sum_1 = 0 For m = 1 To n sum_1 = sum_1 + Solucoes(Dimensao_Sistema_Linear + 1 - m) * _
Triangular_A(Dimensao_Sistema_Linear - n, Dimensao_Sistema_Linear + 1 - m)
Next m Solucoes(Dimensao_Sistema_Linear - n) = (Triangular_A(Dimensao_Sistema_Linear - n, Dimensao_Sistema_Linear + 1) - sum_1) / _
Triangular_A(Dimensao_Sistema_Linear - n, Dimensao_Sistema_Linear - n)
Next n 'Calcula o determinante da matriz [A] 'Este é o produto dos elementos da diagonal da matriz triangular Determinant_1 = 1 'inicia o produto For n = 1 To Dimensao_Sistema_Linear Determinant_1 = Determinant_1 * Triangular_A(n, n) Next n 'define determinante Text2.Text = CStr(Determinant_1) 'define a solução nas caixas de texto textboxes For n = 1 To Dimensao_Sistema_Linear Text1(109 + n).Text = CStr(Solucoes(n)) Next n Exit Sub trataErro: If Err.Number = 6 Then MsgBox "Informe valores válidos para os elmentos da matriz." & vbCrLf & "Se os valores estão corretos então _
pode não existir solução para o sistema.", vbCritical
Else MsgBox "Erro no. = " & Err.Number & vbCrLf & vbCrLf & Err.Description End If End Sub Private Sub Text1_Change(Index As Integer) 'valida a entra dos valores nas células Select Case Index Case 0 To 119 If Not ValidaNumero(Text1(Index).Text) Then Text1(Index).Text = "" Text1(Index).SetFocus End If End Select End Sub Private Function ValidaNumero(strText As String) As Boolean ValidaNumero = CBool(strText = "" _ Or strText = "-" _ Or strText = "-." _ Or strText = "." _ Or IsNumeric(strText)) End Function |
Basta copiar e colar o código acima, lembrando que você tem que incluir no formulário 120 controles TextBox do tipo array numerados de 0 a 119. (Text1(0)...Text1(119)), um combobox e 3 botões de comandos conforme leiaute do formulário do projeto abaixo:
Referências:
Método de Eliminação de Gauss -
http://www.math.ist.utl.pt/~calves/courses/sis-lin/capii11.html
Resolução de Sistemas de Equação Lineares -
http://www.geoma.lncc.br/pdfs/selas.pdf
Até o próximo artigo ... ![]()
José Carlos Macoratti