VB - Operações com Matrizes

VB - Operações com Matrizes

Neste artigo vamos tirar do baú alguns conceitos matemáticos sobre matrizes e mostrar como criar uma interface a mais amigável possível para efetuar operações com matrizes.

Para não complicar demais o código eu vou focar somente as operações de soma , subtração , multiplicação e produto escalar de um número por uma matriz usando números inteiros. Se você detesta matemática não deixe de ler o artigo pois nele vou mostrar como permitir a entra de dados no controle MSFlexGrid.

Os conceitos Matemáticos

Eu particularmente gosto de matemática , e, creio que todo bom programador também deve gostar , afinal conceitos matemáticos estão intimamente relacionados com a arte de programar. Assim o conceito de matrizes é fundamental para qualquer programador. Vamos então recordar os conceitos aprendidos na escola.

a-) O que é uma matriz ?

Matriz de ordem m x n : Para os nossos propósitos, podemos considerar uma matriz como sendo uma tabela rectangular de números reais (ou complexos) dispostos em m linhas e n colunas. Diz-se então que a matriz tem ordem m x n (lê-se: ordem m por n)

Exemplos:

A = ( 1 0 2 -4 5) Uma linha e cinco colunas ( matriz de ordem 1 por 5 ou 1 x 5)

B é uma matriz de quatro linhas e uma coluna, portanto de ordem 4 x 1.

Notas:

1) se m = n , então dizemos que a matriz é quadrada de ordem n.

Exemplo:

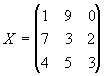
A matriz X é uma matriz quadrada de ordem 3x3 , dita simplesmente de ordem 3 .

2) Uma matriz A de ordem m x n , pode ser indicada como A = (a_ij )_mxn , onde a_ij é um elemento da linha i e coluna j da matriz.

Assim , por exemplo , na matriz X do exemplo anterior , temos a₂₃= 2 , a₃₁= 4 , a₃₃ = 3 , a₃₁ = 4 , a_3,2 = 5 ,

Vamos ver a seguir o conceito de produto de matrizes.

b-) Produto de matrizes

Para que exista o produto de duas matrizes A e B , o número de colunas de A , tem de ser igual ao número de linhas de B.

A_m_x_n x B_n_x_q= C_m_x_q

Se a matriz A tem ordem m x n e a matriz B tem ordem n x q , a matriz produto C tem ordem m x q .

Vamos mostrar o produto de matrizes com um exemplo:

Onde L1C1 é o produto escalar dos elementos da linha 1 da 1ª matriz pelos elementos da coluna1 da segunda matriz, obtido da seguinte forma:

L1C1 = 3.2 + 1.7 = 13. Analogamente, teríamos para os outros elementos:
L1C2 = 3.0 + 1.5 = 5
L1C3 = 3.3 + 1.8 = 17
L2C1 = 2.2 + 0.7 = 4
L2C2 = 2.0 + 0.5 = 0
L2C3 = 2.3 + 0.8 = 6
L3C1 = 4.2 + 6.7 = 50
L3C2 = 4.0 + 6.5 = 30
L3C3 = 4.3 + 6.8 = 60, e, portanto, a matriz produto será igual a:

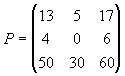
Observe que o produto de uma matriz de ordem 3x2 por outra 2x3, resultou na matriz produto P de ordem 3x3.

Nota: O produto de matrizes é uma operação não comutativa, ou seja: A x B # B x A

c-) Soma e Subtração de matrizes

Com os conceitos acima creio que não precisarei entrar em mais detalhes , assim , para que a operação de adição e subtração entre duas matrizes seja possível , elas devem ser da mesma ordem , ou seja, deverá possuir o mesmo número de linhas e de colunas.

Assim se a ordem da matriz A for m x n e a da matriz B p x q , para que a soma seja possível teremos que ter m=p e n=q.

A soma ou subtração entre duas matrizes é realizada entre a soma dos elementos da linha 1 da 1ª matriz pelos elementos da linha 1 da segunda matriz e assim sucessivamente.

Resumindo temos que A soma de duas matrizes A e B, ambas de ordem m x n, é uma matriz C de mesma ordem, em que cada elemento é a soma dos elementos correspondentes em A e B.

d-) Produto escalar de um número por uma matriz

Multiplicar uma matriz A por um número "k" é obter uma matriz B de mesma ordem de A, formada pelos elementos de a multiplicados por k.

VB - Matrizes

Vou aproveitar a oportunidade para recordar alguns dos conceitos sobre'arrays' no VB. Vamos lá...

No VB uma 'array' ( matriz ou arranjo) faz referência a um conjunto de variáveis de mesmo nome que identificamos por um indíce numérico com um limite inicial e um final. Todos os elementos da matriz possui o mesmo tipo de dados. Um 'array' pode ter um tamanho fixo ou pode variar dinamicamente.

Um 'array' de tamanho fixo é criado usando o comando Dim usando a seguinte sintaxe:Dim NomeMatriz(indice)

Ex: Dim Matriz(5) -A matriz terá os elementos :Matriz(0), Matriz(1), Matriz(2) , Matriz(3) , Matriz(4)

Geralmente o índice inicial é zero (podemos alterar isto usando o comando Option Base 1 no módulo da aplicação) , mas podemos definir o índice incial e final na declaração do array:Dim Matriz( 1 to 20).

Para criar uma matriz dinâmica basta declarar a matriz sem definir os limites: ex:Dim Matriz()

Em seguida , quando precisar , basta redimensionar a matriz usando o comando Redim. Ex:Redim Matriz(20)

O comando Redim todos os valores armazenados na matriz são perdidos , se quiser , manter os valores já atribuídos ao array deve usar a cláusula :Preserve. Ex: Redim Preserve Matriz(20)

A interface com o usuário

Se você chegou até aqui parabéns , vamos agora mostrar como criar um programa no Visual Basic , é claro , que efetue as operações com matrizes acima descritas. A primeira coisa que vou mostrar será a interface com o usuário , ou seja os formulários usados na aplicação.

Nosso projeto terá os seguintes formulários :

frmmatrizes.frm - o formulário principal onde iremos exibir os controles para entrada de dados do usuário
frmresultado.frm - o formulário onde iremos exibir o resultado da operação com matrizes
prodmatriz.bas - o módulo onde iremos declarar as variáveis globais.

Vou mostrar agora as três visões da aplicação ; primeiro as visões do formulário frmmatrizes.frm:

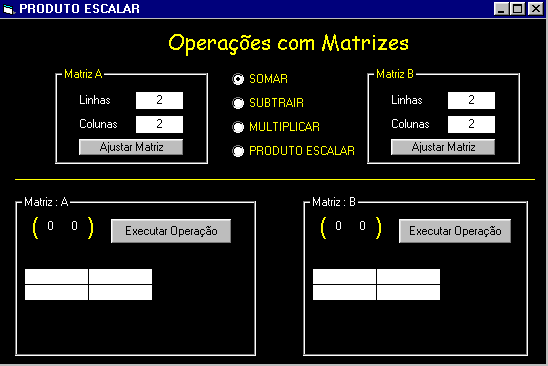	- frmmatrizes.frm - Esta é a visão principal da aplicação para as operações somar/subtrair e multplicar , nela temos além das caixas de texto onde o usuário informa o número de linhas e de colunas para cada matriz , dois controles MSFlexgrid onde o usuário irá digitar os valores para cada célula da matriz.

	- frmmatrizes.frm -Esta é a visão do produto escalar de um número inteiro por uma matriz.

	- frmresultado.frm - Este formulário exibe o resultado das operações entre as matrizes.

O codigo da aplicação

Não vou comentar todo o código da aplicação , vou me ater somente na entrada de dados do controle MSFlexgrid e no código que realiza as operações de soma , subtração , produto e produto escalar.

- A primeira coisa a fazer é escolher a operação e a seguir informar o número de linhas e colunas para cada matriz. Ao clicar no botão - informar valores - o sistema cria automaticamente via controle msflexgrid uma grade com o mesmo número de linhas e colunas informadas pelo usuário.(lembrando que no caso do msflexgrid o índice inicial é zero). O código que faz esta operação é dado a seguir:

Private Sub define_tamanho_matrizA()
  grdgrid1.Rows = Int(txtlinhas1(1).Text)
  grdgrid1.Cols = Int(txtcolunas1(2).Text)

   For i = 0 To grdgrid1.Rows - 1
     grdgrid1.RowHeight(i) = 300
   Next
   For j = 0 To grdgrid1.Cols - 1
     grdgrid1.ColWidth(j) = 700
   Next
End Sub

O código acima - Define a grade usando os valores informados para o número de linhas e colunas , e também define o tamanho de cada célula da grade.

- O código de entrada de dados (ver abaixo) via controle MSFlexgrid. O usuário clica na célula e digita os valores e tecla ENTER para ir para a próxima célula.

'entrada de valores na Matriz A - grdgrid1
Private Sub grdGrid1_KeyPress(KeyAscii As Integer)
'se o caractere for um numero, ponto ou sinal de menos então permite a entrada
If KeyAscii > 47 And KeyAscii < 58 Or KeyAscii = 46 Or KeyAscii = 45 Or _
KeyAscii = 43 Or KeyAscii = 105 Or KeyAscii = 106 Then
   grdgrid1.Text = grdgrid1.Text + Chr(KeyAscii)
   cnt = cnt + 1
ElseIf KeyAscii = 8 Then 'se for um retrocesso, remove o último caractere entrado
  If cnt > 0 Then
    cnt = cnt - 1
    grdgrid1.Text = Left(grdgrid1, cnt)
  End If
  'se pressione enter entao move para a proxima celula
ElseIf KeyAscii = 13 Then
  If grdgrid1.Col < grdgrid1.Cols - 1 Then 'move para direita ate alcancar o fim da linha
     grdgrid1.Col = grdgrid1.Col + 1
  Else
     grdgrid1.Col = 0
     If grdgrid1.Row < grdgrid1.Rows - 1 Then 'entao vai para proxima linha
        grdgrid1.Row = grdgrid1.Row + 1
     Else
        grdgrid1.Row = 0 'quando alcanca a ultima linha volta para primeira celula
        grdgrid1.Col = 0
     End If
  End If
ElseIf KeyAscii = 67 Or KeyAscii = 99 Then ' se pressionear c ou C limpa a celula
     grdgrid1.Text = ""
ElseIf KeyAscii = 61 Then
   KeyAscii = 43
   grdgrid1.Text = grdgrid1.Text + Chr(KeyAscii)
   cnt = cnt + 1
End If
End Sub

O código captura a tecla que o usuário digitou e verifica se ela tem um valor válido (número, sinal de -/+) ou se o usuário teclou o retrocesso.(KeyAscii = 8) ; neste caso é permitido a correção do valor informado.

Para limpar a célula basta digitar o caractere C ou c. (KeyAscii = 67 Or KeyAscii = 99)

Ao digitar a tecla - ENTER- (Keyscii = 13) o foco muda para a célula seguinte até o final do grid.

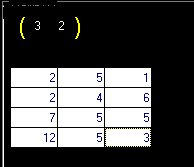
Este código permite que o usuário informe os valores em cada célula do MSFLexgrid ; cada célula representa uma linha e coluna da matriz. Abaixo uma visão da entrada de dados em uma matriz 4x3 usando o controle MSFlexgrid.

- Quando o usuário informa o número de linhas e colunas e clica no botão informar valores , um grid com 4 linhas e 3 colunas e exibido para entrada de dados.

- na parte superior temos a indicação da posição célula representando um elemento da linha i e da coluna j.

Após informar os valores para cada matriz basta clicar no botão para realizar a operação selecionada. Vejamos agora o código de cada operação.

- Produto de matrizes

Public Function ProdutoMatriz()

Dim i As Integer
Dim j As Integer
Dim k As Integer
Dim m As Integer
Dim produto As Single
Dim resultado As Single

ReDim MatrizResultado(grdgrid1.Rows, grdgrid2.Cols)

For i = 0 To grdgrid1.Rows - 1
  For k = 0 To grdgrid2.Cols - 1
    resultado = 0
    For j = 0 To grdgrid1.Cols - 1
      If grdgrid1.TextMatrix(i, j) = "" Then
        grdgrid1.TextMatrix(i, j) = 0
      End If
      If grdgrid2.TextMatrix(j, k) = "" Then
         grdgrid2.TextMatrix(j, k) = 0
      End If
      produto = Val(grdgrid1.TextMatrix(i, j)) * Val(grdgrid2.TextMatrix(j, k))
      resultado = resultado + produto
    Next j
    MatrizResultado(i, k) = resultado
  Next k
Next i
frmresultado.Show
End Function

Redimensionamos a variável MatrizResultado para conter o número de linhas da matriz A e o número de colunas da matriz B - ReDim MatrizResultado(grdgrid1.Rows, grdgrid2.Cols)

Em um loop percorremos as linhas e colunas e multiplicamos os elementos da primeira linha pelos elementos da primeira coluna sucessivamente ; e armazenamos o resultado na variável produto ; a cada mudança de linha atribuimos o valor acumulado á variável - MatrizResultado(i,j).

- Soma de matrizes

O codigo para soma de matrizes é dado a seguir , para subtração basta mudar o sinal da operação de + para - .

Public Function SomarMatriz()

Dim i As Integer
Dim j As Integer

ReDim MatrizResultado(grdgrid1.Rows, grdgrid2.Cols)

  For i = 0 To grdgrid1.Rows - 1
    For j = 0 To grdgrid2.Cols - 1
      resultado = 0
      If grdgrid1.TextMatrix(i, j) = "" Then
         grdgrid1.TextMatrix(i, j) = 0
      End If
      If grdgrid2.TextMatrix(i, j) = "" Then
         grdgrid2.TextMatrix(i, j) = 0
      End If
      resultado = Val(grdgrid1.TextMatrix(i, j)) + Val(grdgrid2.TextMatrix(i, j))
      MatrizResultado(i, j) = resultado
   Next j
Next i
frmresultado.Show
End Function

O codigo acima soma os elementos de cada linha da matriz A com os elementos de cada linha da Matriz B. O resultado é armazenado na variável - MatrizResultado(i,j).

- Produto de um escalar por uma matriz

Public Function EscalarMatriz()

Dim i As Integer
Dim j As Integer

ReDim MatrizResultado(grdgrid1.Rows, grdgrid2.Cols)

For i = 0 To grdgrid1.Rows - 1
  For j = 0 To grdgrid1.Cols - 1
    resultado = 0
    If grdgrid1.TextMatrix(i, j) = "" Then
       grdgrid1.TextMatrix(i, j) = 0
    End If
    If grdgrid2.TextMatrix(i, j) = "" Then
       grdgrid2.TextMatrix(i, j) = 0
    End If
    resultado = (Val(grdgrid1.TextMatrix(i, j)) * Val(txtescalar.Text))
    MatrizResultado(i, j) = resultado
  Next j
Next i
frmresultado.Show
End Function

O código acima multiplica da elemento da matriz A pelo número informado e armazena o resultado na variável MatrizResultado(i,j).

Obs: Perceba que o código abaixo aparece em todas as operações ; ele apenas garante que se alguma célula não possuir um valor o valor atribuído será o número zero.

 If grdgrid1.TextMatrix(i, j) = "" Then
    grdgrid1.TextMatrix(i, j) = 0
 End If
 If grdgrid2.TextMatrix(i, j) = "" Then
    grdgrid2.TextMatrix(i, j) = 0
 End If

- Apresentando o resultado da operação

No final de cada operação o formulário - frmresultado.frm - é invocado para exibir o resultado, vejamos o seu código:

Private Sub Form_Load()

grdgrid3.Rows = frmmatrizes.grdgrid1.Rows
grdgrid3.Cols = frmmatrizes.grdgrid2.Cols

For i = 0 To grdgrid3.Rows - 1
   grdgrid3.RowHeight(i) = 300
Next
For j = 0 To grdgrid3.Cols - 1
   grdgrid3.ColWidth(j) = 700
Next

For i = 0 To grdgrid3.Rows - 1
  For j = 0 To grdgrid3.Cols - 1
    grdgrid3.TextMatrix(i, j) = MatrizResultado(i, j)
  Next j
Next i

End Sub

Neste código primeiro é criado o grid com o número de linhas da Matriz A e o número de colunas da Matriz B:

grdgrid3.Rows = frmmatrizes.grdgrid1.Rows
grdgrid3.Cols = frmmatrizes.grdgrid2.Cols

a seguir formatamos o tamanho de cada célula e atribuímos os valores armazenados na matriz MatrizResultado(i,j) a cada célula do grid.

For i = 0 To grdgrid3.Rows - 1
 For j = 0 To grdgrid3.Cols - 1
   grdgrid3.TextMatrix(i, j) = MatrizResultado(i, j)
 Next j
Next i

Abaixo vamos mostra a sequência de uma operação de produto de matrizes :

A matriz A = 5 x 3
A matriz B = 3 X 4

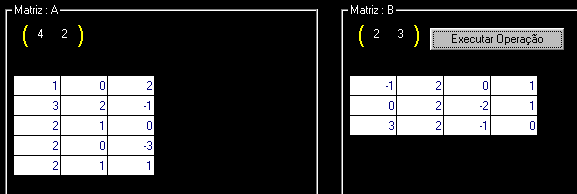O resultado será uma matriz da ordem : 5 x 4 conforme abaixo :

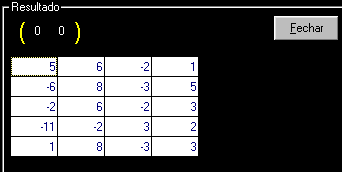
Neste artigo além de aprender alguns conceitos matemáticos importantes também aprendemos outra forma de usar o MSFlexGrid para entrada de dados.

Agora acabei , até o próximo artigo sobre VB e a matemática...!!! (o projeto completo esta no super CD VB)

José Carlos Macoratti