A ideia é usar a letra O seguida de uma função sobre n que descreva esse crescimento do algoritmo. Quanto mais rapidamente crescer o número de operações para processar os itens, "pior" é o desempenho do algoritmo (pois ele executa mais instruções e, portanto, mais - é "mais complexo").
Em palavras simples, a notação Big O descreve a complexidade do seu código usando termos algébricos e é uma forma de classificar o quanto a sua função ou algoritmo é escalável.
Usando esta notação podemos determinar qual será o comportamento de um algoritmo no pior cenário ou quanto tempo ele gasta para ser concluído com base em seus valores de entrada.
Geralmente estamos preocupados com o tempo que que será gasto para executar o código e isso pode depender de diversos fatores como : velocidade do computador, linguagem de programação usada, compilador que traduziu o programa, algoritmo usado para implementar o código, dentre outros fatores.
Para dimensionar o tempo gasto com base apenas no algoritmo usado, podemos considerar a quantidade dos termos ou o tamanho da entrada dos dados e o quão rápido a função vai crescer com base neste tamanho. (Isso é conhecido como taxa de crescimento.)
Em relação ao tamanho da entrada dos dados e do tempo gasto podemos considerar como ele pode afetar o desempenho do código usando 4 cenários :
- constante
- linear
- exponencial
- logaritmicos
Vamos analisar cada um destes cenários...
Antes de iniciar temos que entender que todas as notações Big O envolvem o algoritmo O(f(n)), e, isso significa que o número de operações simples que o computador precisa fazer diminui à medida que o computador avança em n.
1- Cenário Constante
Neste cenário temos que as funções não dependem da quantidade de valores de entrada informados e o tempo gasto para executar o código será o mesmo, ou seja, o tempo de resposta vai se manter o mesmo independente do tamanho da entrada.
Como exemplo para este cenário temos o seguinte código C#:
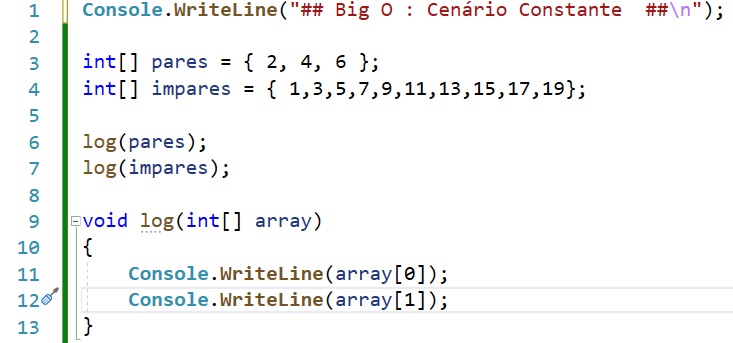
Neste código independente da quantidade de valores que array receber o método ou função vai sempre imprimir os valores das duas primeiras posições e assim o tempo para executar esta função vai se manter sempre o mesmo.
O tipo de notação dessa função é O(1) e abaixo temos o gráfico mostrando o comportamento em relação ao tempo gasato desta função :

Se um algoritmo tem um O(1), isso significa que, não importa qual seja o valor de n, a quantidade de operações necessárias para resolver o problema permanece constante.
2- Cenário Linear
Neste cenário temos os algoritmos lineares que realizam uma interação com cada valor informado na entrada. Neste caso a quantidade de operações realizadas será correspondente ao número de valores de entrada informados.
Como exemplo temos o seguinte código C#:
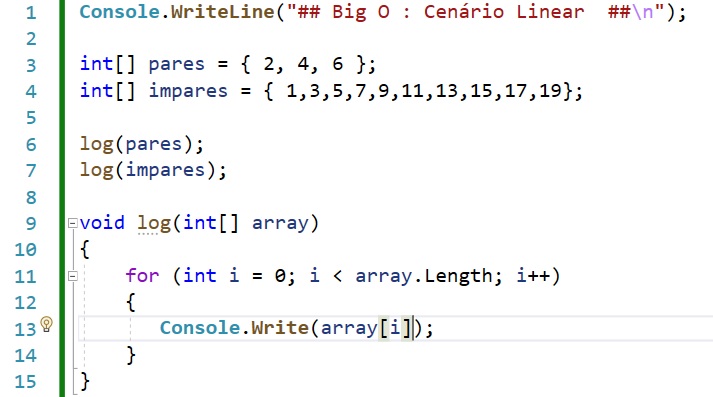
Agora temos que o método ou função vai imprimir cada valor do array, e assim, se a entrada de dados aumentar o tempo gasto para executar o código também vai aumentar.
Esse tipo de algoritmo possui uma notação O(n), onde “n” representa o número de valores passados na entrada. Abaixo o gráfico que representa este comportamento:

Desta forma se uma operação tem uma anotação O(n) (pronuncia-se 'O de N'), o que isso significa é que, à medida que 'n' aumenta, também aumenta a quantidade de operações necessárias para concluir o problema.
3- Cenário Exponencial
No cenário exponencial temos que que o número de interações e o tempo de execução vai aumentar de forma exponencial.
Para este cenário vamos considerar o código C# a seguir:

Neste código para cada iteração feita com um elemento do array estamos imprimindo uma combinação possível do elemento com os demais valores. Assim para cada elemento entrado no array, o número de iterações e o tempo de execução vai aumentar de forma exponencial.
Assim esses algoritmos são os mais custosos e os menos eficientes.
Este algoritmo possui uma notação O(n²) representado pelo seguinte gráfico:
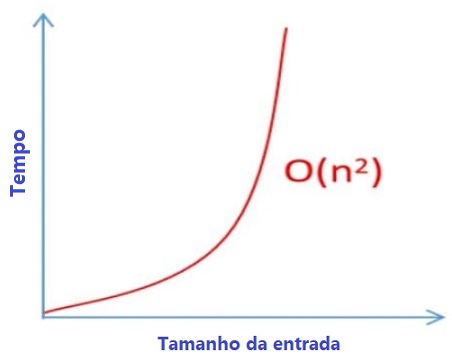
Uma operação O(n) dentro de uma operação O(n) é uma operação O(n * n), ou seja, uma operação O(n ²). Esta é a mais lenta e menos eficiente e, portanto, a menos desejável notação Big O ao considerar a complexidade do tempo.
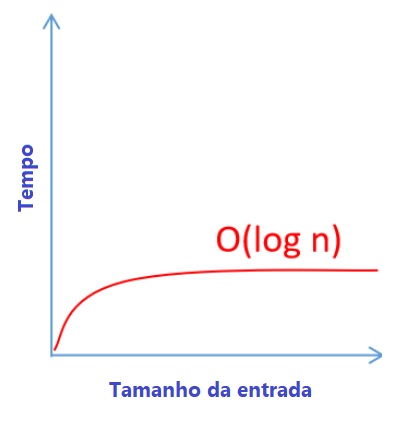
4- Cenário Logaritmico
No cenário logaritmico temos os algoritmos que são considerados de alto desempenho pois oferecem uma opção de interação muito eficiente para um grande número de entrada de valores.
Como exemplo de código para este cenário temos uma implementação da busca binária usando a abordagem interativa em C#:

Neste código, em cada busca feita o método vai receber dois valores como parâmetros :
- Oo primeiro é um array de elementos (que já deve estar ordenado);
- O segundo é o valor que queremos localizar no array;
A busca binária possui um tempo de complexidade logarítmico, pois em cada operação eliminamos os valores de entrada que não satisfazem as condições de busca pela metade o que faz com que apenas verifiquemos uma fração de valores dos dados de entrada para encontrar o valor procurado.
O gráfico que representa este cenário é o seguinte: