![]() C#
- Algoritmos de ordenação - II
C#
- Algoritmos de ordenação - II
 |
Hoje vamos iniciar a apresentação dos algoritmos de ordenação usando a linguagem C#. |
Continuando o artigo anterior vamos tratar agora com alguns algoritmos de ordenação.
O objetivo principal de um algoritmo de ordenação é realizar a ordenação de uma lista de valores.
Podemos usar os seguintes métodos para os algoritmos de ordenação:
Conhecer a lógica dos principais algoritmos de ordenação é um conceito que todo o profissional de TI deve possui, é como saber a tabuada. (Pelo menos os principais)
Eu vou focar nos seguintes métodos de ordenação : Shell Sort, Insertion Sort, Selection Sort, Bubble Sort e QuickSort.
A ideia é aprender como esses algoritmos são codificados na linguagem C#, e entender o essencial para analisar seu desempenho, tanto teórica quanto experimentalmente.
Eu não vou me ater a um estudo teórico dos algoritmos, se você desejar se aprofundar vou deixar o link para dois livros :
Em todos os exemplos de código estaremos usando um projeto do tipo Console(.NET Core) no VS 2019 Community e a linguagem C#

Ordenação com Bubble Sort
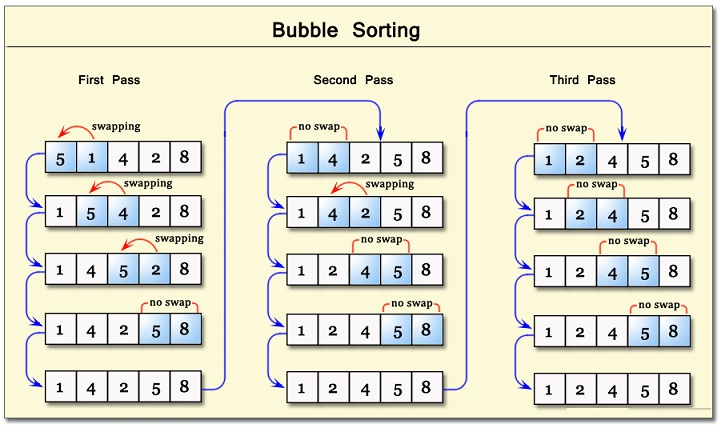
O algoritmo Bubble Sort funciona varrendo repetidamente o array, trocando elementos adjacentes que estão fora de ordem. Observando este trabalho com um Console.WriteLine() colocado estrategicamente no loop externo, você verá que a matriz classificada cresce da direita para a esquerda.
Cada varredura
pega o maior elemento restante e se move para a direita o máximo que pode.
Portanto, não é necessário percorrer todo o array a cada varredura, mas apenas o
início da parte ordenada.
Definimos o número de inversões como o número de pares de elementos que estão
fora de ordem. Eles não precisam ser adjacentes. Se
dados[7] > dados[16], isso é uma inversão.
Cada vez que uma
inversão é necessária, também dizemos que há movimentação de dados
correspondente. Se você observar o código do método
TrocarValores(), verá que uma troca requer três movimentos para ocorrer,
o que acontece muito rapidamente na maioria dos processadores, mas ainda
representa um custo significativo.
Assim pode haver no máximo
N*(N-1)/2 inversões na matriz de comprimento N. O
número máximo de inversões ocorre quando a matriz é classificada em ordem
reversa e não possui elementos iguais.
Cada troca no Bubble Sort remove precisamente uma inversão; portanto, o
Bubble Sort requer O(N2)
trocas.
A seguir uma possível implementação feita na linguagem C#:
using System;
namespace BubbleSort
{
class Program
{
static void Main(string[] args)
{
int[] numeros = { 230, 45, 345, 4, 324, 90, 76, 34, 67 };
Console.WriteLine("######## Ordenação com Bubble Sort ########\n");
Console.WriteLine("Array original\n");
foreach (int numero in numeros)
Console.Write($"{numero} ");
Console.WriteLine("\n\nOrdenando o array usando Bubble Short\n");
int[] arrayOrdenado = IntArrayBubbleSort(numeros);
Console.WriteLine("Array Ordenado\n");
foreach (int numero in arrayOrdenado)
Console.Write($"{numero} ");
Console.ReadLine();
}
public static int[] IntArrayBubbleSort(int[] data)
{
int i, j;
int N = data.Length;
for (j = N - 1; j > 0; j--)
{
for (i = 0; i < j; i++)
{
if (data[i] > data[i + 1])
TrocarValores(data, i, i + 1);
}
}
return data;
}
public static int[] TrocarValores(int[] arrayDados, int m, int n)
{
int temp;
temp = arrayDados[m];
arrayDados[m] = arrayDados[n];
arrayDados[n] = temp;
return arrayDados;
}
}
}
|
Você pode simplificar o código acima usando apenas um método e mudando a lógica usada no método TrocarValores para o método:
public static int[] OrdenacaoBubbleSort(int[] vetor)
{
int tamanho = vetor.Length;
int comparacoes = 0;
int trocas = 0;
for (int i = tamanho - 1; i >= 1; i--)
{
for (int j = 0; j<i; j++)
{
comparacoes++;
if (vetor[j] > vetor[j + 1])
{
int aux = vetor[j];
vetor[j] = vetor[j + 1];
vetor[j + 1] = aux;
trocas++;
}
}
}
return vetor;
}
|
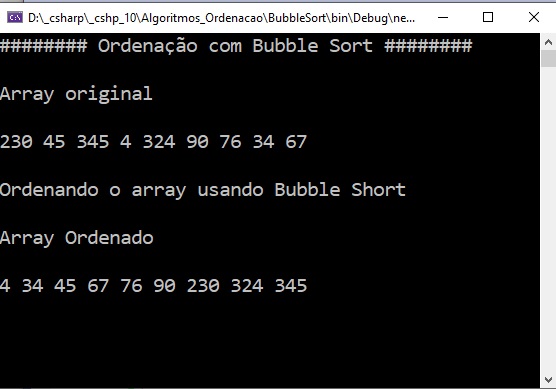
O resultado obtido será o mesmo :
Pegue o projeto
completo aqui: ![]() Algoritmos_Ordenacao.zip
Algoritmos_Ordenacao.zip
Na próxima parte do artigo vamos continuar com os algoritmos de ordenação.
"Mas o fruto do
Espírito é: amor, gozo, paz, longanimidade, benignidade, bondade, fé, mansidão,
temperança.
Contra estas coisas não há lei."
Gálatas 5:22,23
Referências:
O tratamento de datas no VB.NET
VB .NET - Datas, horas: conceitos e operações
C# - Programação Assíncrona como : Asycn e Task
Algoritmos de ordenação
NET - Números Perfeitos
SQL - O Algoritimo Soundex
C# - Estrutura de dados - Algorítmos
C# - Operadores Lógicos
C# - Apresentando Arrays
C # - Avaliando Expressões
C# - Resolvendo 10 problemas de matemática
VB .NET - Usando Reflection
C# - Usando Reflection na prática - I
C# - Reflection e o Late Binding
C# - Usando delegates na prática - Ordenação
C# - Algoritmos de ordenação de dados : Inserção