|
|
 |
Neste artigo eu vou apresentar a conjectura de Goldback e uma implementação feita na linguagem C# e VB .NET que mostra como fazer a sua verificação. |
 |
Uma conjectura matemática é uma proposição que muitos matemáticos acham que deve ser verdadeira, porém, ainda não conseguiram prová-la.
A conjetura de Goldbach,
proposta pelo matemático prussiano Christian Goldbach,
é um dos problemas mais antigos não resolvidos da matemática, mais precisamente
da teoria dos números.
A famosa Conjetura de Goldbach diz que :
todo número par maior que 3 é
igual a soma de dois números primos.
Por exemplo:
4 = 2 + 2;
6 = 3 + 3;
8 = 5 + 3;
10 = 3 + 7 ;
12 = 5 + 7; etc.
Verificações por computador já confirmaram a conjetura de Goldbach para vários números. No entanto, a efetiva demonstração matemática ainda não ocorreu.
Mas para que a
conjectura vire um teorema é preciso que alguém encontre uma prova que assegure
que qualquer um dos infinitos números pares pode ser escrito como soma de dois
primos. A proposição é muito simples, mas, até hoje, ninguém conseguiu
demonstrá-la.
O melhor resultado até agora foi dado por Olivier Ramaré
em 1995: todo número par é a soma de no máximo 6 números primos.
Se você quiser pode testar a conjetura de Goldback para alguns números pares.
Uma forma divertida de fazê-lo é acessando ao jogo da Conjetura de Goldbach no seguinte site: http://nautilus.fis.uc.pt/mn/goldbach/index.html.
Fontes : Wikipedia e http://www.uff.br/sintoniamatematica (consultados em janeiro de 2015)
Agora vamos a uma implementação feita na linguagem C# que pode ser usada para testar (e não provar) a conjetura de Goldback para alguns números pares inteiros:
Nota: Em 1930 o matemático soviético Lev Genrikhovich Shnirelman provou que todo número natural pode ser expresso como soma de até 20 números primos; e em 1973 o matemático chinês Chen Jing Run provou que todo número par suficientemente grande é soma de um número primo com outro número que é obtido como produto de no máximo dois primos.
Recursos usados:
Nota: Baixe e use a versão Community 2015 do VS ela é grátis e é equivalente a versão Professional.
Criando o projeto no VS Community
Abra o VS Community 2015 e clique em New Project;
Selecione a linguagem Visual C# e o template Console Application;
Informe o nome Goldback_Conjectura_CSharp e clique no botão OK;
A seguir inclua o código abaixo no arquivo Program.cs:
using System;
namespace Goldbach_Conjectura
{
/// <summary>
/// Calcula todos os primos menor que N e tenta expressar N como uma
/// coma de dois números primos
/// A conjecture de Goldbach afirma que isto é sempre possível se N
/// é par e maior que dois
/// Quando N for impar ele é chamado de um primo par
/// </summary>
class Program
{
static void Main(string[] args)
{
Console.WriteLine(" ****** Verificação da Conjectura de Goldback - CSharp *****\n ");
while (true)
{
//o primeiro número que atende o critério definido
int N = 4;
int resto;
Console.WriteLine("Digite um número inteiro PAR :"); // Prompt
string numero = Console.ReadLine(); // Pega a entrada do usuário
if (numero == "sair") // verifica se quer sair
{
break;
}
else
{
//converte a entrada em um número inteiro
try
{
N = Convert.ToInt32(numero);
//Sai se digitar um número impar
//resto = (N % 2 );
//if ( resto != 0 )
//{
// break;
//}
}
catch
{
break;
}
}
Boolean[] EPrimo = new Boolean[N];
for (int i = 2; i < N; i++)
EPrimo[i] = true;
// determina os primos < N usando o algoritimo de Crivo de Eratosthenes
for (int i = 2; i * i < N; i++)
{
if (EPrimo[i])
{
for (int j = i; i * j < N; j++)
EPrimo[i * j] = false;
}
}
// conta os primos
int primos = 0;
for (int i = 2; i < N; i++)
{
if (EPrimo[i])
{
primos++;
}
}
Console.WriteLine("----------------------------------------------");
// armazena os primos em uma lista
int[] list = new int[primos];
int n = 0;
for (int i = 0; i < N; i++)
{
if (EPrimo[i])
{
list[n++] = i;
}
}
// verifica se o numero N pode ser expresso como soma de dois primos
int left = 0, right = primos - 1;
while (left <= right)
{
if (list[left] + list[right] == N)
break;
else if
(list[left] + list[right] < N) left++;
else
right--;
}
if (list[left] + list[right] == N)
{
Console.WriteLine(N + " = " + list[left] + " + " + list[right]);
Console.WriteLine("----------------------------------------------");
}
else
{
Console.WriteLine(N + " não pode ser expresso como soma de dois números primos");
}
}
}
}
}
|
Nota: Esse código foi baseado na implementação Java obtida neste site: http://introcs.cs.princeton.edu/java/14array/Goldbach.java
Agora é só alegria...
Executando o projeto vemos algumas verificações feitas conforme a figura abaixo:
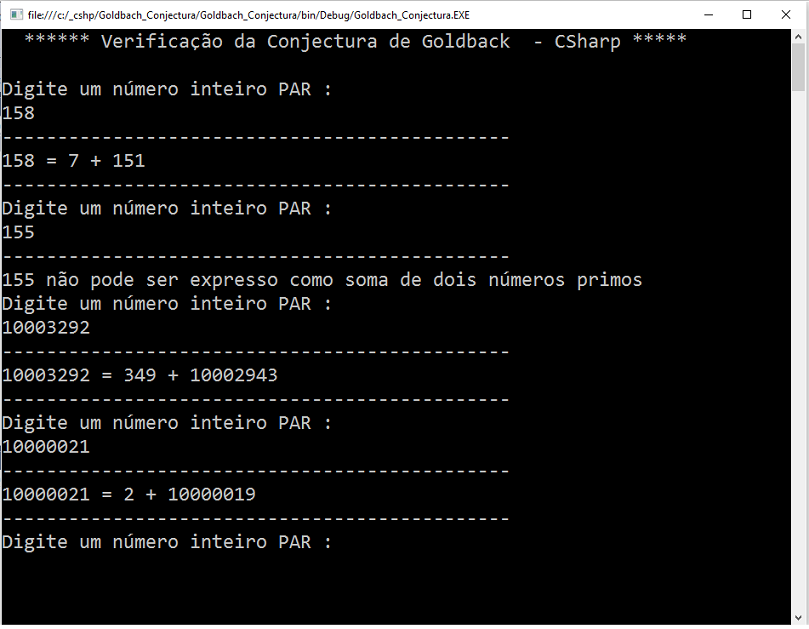 |
Agora vamos fazer a implementação para a linguagem VB .NET com base no código acima.
No menu File clique em Add -> New Project e selecione a linguagem Visual Basic -> Console Application e informe o nome Goldback_Conjectura_VBNET;
A seguir inclua o código abaixo no módulo Module1 :
Module Module1
Sub Main()
Console.WriteLine(" ****** Verificação da Conjectura de Goldback - VB .NET *****" & vbLf & " ")
While True
'o primeiro número que atende o critério definido
Dim N As Integer = 4
Dim resto As Integer
'espera a entrada do usuário
Console.WriteLine("Digite um número inteiro PAR :")
' Prompt
Dim numero As String = Console.ReadLine()
' Pega a entrada do usuário
If numero = "sair" Then
' verifica se quer sair
Exit While
Else
'converte a entrada em um número inteiro
Try
N = Convert.ToInt32(numero)
'sai se for um número impar
'resto = (N Mod 2)
'If resto <> 0 Then
' Exit Try
'End If
Catch
Exit Try
End Try
End If
Dim EPrimo As [Boolean]() = New [Boolean](N - 1) {}
For x As Integer = 2 To N - 1
EPrimo(x) = True
Next
' determina os primos < N usando o algoritimo de Crivo de Eratosthenes
Dim i As Integer = 2
While i * i < N
If EPrimo(i) Then
Dim j As Integer = i
While i * j < N
EPrimo(i * j) = False
j += 1
End While
End If
i += 1
End While
' conta os primos
Dim primos As Integer = 0
For y As Integer = 2 To N - 1
If EPrimo(y) Then
primos += 1
End If
Next
Console.WriteLine("----------------------------------------------")
' armazena os primos em uma lista
Dim list As Integer() = New Integer(primos) {}
Dim w As Integer = 0
For y As Integer = 0 To N - 1
If EPrimo(y) Then
list(System.Math.Max(System.Threading.Interlocked.Increment(w), w - 1)) = y
End If
Next
' verifica se o numero N pode ser expresso como soma de dois primos
Dim left As Integer = 0, right As Integer = primos - 1
While left <= right
If list(left) + list(right) = N Then
Exit While
ElseIf list(left) + list(right) < N Then
left += 1
Else
right -= 1
End If
End While
If list(left) + list(right) = N Then
Console.WriteLine(N.ToString() + " = " + list(left).ToString + " + " + list(right).ToString)
Console.WriteLine("----------------------------------------------")
Else
Console.WriteLine(N.ToString + " não pode ser expresso como soma de dois números primos")
End If
End While
End Sub
End Module
|
Nota: A implementação VB .NET foi feita usando uma ferramenta de conversão de C# para VB .NET e precisa ser melhor verificada.
Pegue o projeto
completo aqui: ![]() Goldbach_Conjectura.zip
Goldbach_Conjectura.zip
Porque do céu se manifesta a ira de Deus sobre toda a impiedade e injustiça dos
homens, que detêm a verdade em injustiça.
Porquanto o que de Deus se pode conhecer neles se manifesta, porque Deus lho
manifestou.
Porque as suas coisas invisíveis, desde a criação do mundo, tanto o seu eterno
poder, como a sua divindade, se entendem, e claramente se veem pelas coisas que
estão criadas, para que eles fiquem inescusáveis;
Romanos 1:18-20
|
Veja os
Destaques e novidades do SUPER DVD Visual Basic
(sempre atualizado) : clique e confira !
Quer migrar para o VB .NET ?
Quer aprender C# ??
Quer aprender os conceitos da Programação Orientada a objetos ? Quer aprender o gerar relatórios com o ReportViewer no VS 2013 ? |
Gostou ? ![]() Compartilhe no Facebook
Compartilhe no Facebook
![]() Compartilhe no Twitter
Compartilhe no Twitter
Referências:
Super DVD Vídeo Aulas - Vídeo Aula sobre VB .NET, ASP .NET e C#
C# - Calculando os fatores primos de um número - Macoratti ...
C# - Os doze trabalho de Hércules - 12 Desafios cumpridos ...