VB - Calculando Combinações, Permutações e Fatorial de um número

Hoje vamos falar sobre Permutações, Combinações e Fatorial.

Se você não fugiu da escola, deve lembrar das aulas de matemática quando algum dia alguém tentou lhe ensinar a calcular permutações.

Vamos então começar lembrando a teoria iniciando com o conceito sobre arranjos...

Arranjos

Arranjos são agrupamentos nos quais a ordem dos elementos faz diferença.

Por exemplo, os números de três algarismos formados pelos elementos {1,2 e 3} são:

312, 321, 132, 123, 213, 231

Esse agrupamento é um arranjo, pois a ordem dos elementos 1, 2 e 3 é diferente; È considerado arranjo simples, pois os elementos não se repetem.

Para que tenhamos arranjos simples é preciso ter um conjunto de elementos distintos com uma quantidade qualquer de elementos, sendo que os arranjos simples formados irão possuir n elementos, e essa quantidade será igual ou menor que a quantidade de elementos do conjunto.

Permutação

O conceito de permutação expressa a idéia de que objetos distintos podem ser arranjados em inúmeras ordens distintas.

Assim seja um conjunto A com n elementos, chamamos de permutação a todo arranjo com n elementos retirados de A.

A cada um dos agrupamentos que podemos formar com certo número de elementos distintos, tal que a diferença entre um agrupamento e outro se dê apenas pela mudança de posição entre seus elementos, damos o nome de permutação simples.

Exemplos:

1) Seja A um conjunto com os elementos {a, b, c}.

As permutações possíveis de A são: {(a,b,c);(a,c,b);(b,a,c);(b,c,a);(c,a,b);(c,b,a)}. Total de 6 permutações.

2) Quantos anagramas possui a palavra OBA ?

As permutações da palavra são: {(OBA;(OAB);(BAO);(BOA);(ABO);(AOB)}. Total de 6 permutações.

Assim para obter o número de permutações com m elementos distintos de um conjunto, basta escolher os m elementos em uma determinada ordem.

O número de permutações de m elementos será expresso por : P(m)

A expressão para seu cálculo será dada por:

P(m) = m(m-1)(m-2)...(m-p+1)...3.2.1

Podemos também escrever :    A(m,m) = P(m)

O Arranjo de m elementos dos quais m elementos participam é igual a Permutação destes elementos.

Uma forma simplificada de expressar a permutação de m elementos é através do fatorial: P(m) = m!

Este símbolo de exclamação posto junto ao número m é lido como o fatorial de m, onde m é um número natural.

O fatorial de um número inteiro não negativo pode ser definido de uma forma recursiva através da função P=P(m) ou com o uso do sinal de exclamação:

(m+1)! = (m+1).m!     Ex: 3! = 3.2.1!   =>  que é a mesma coisa que : 3.2.1 = 6

Nota : Lembrando que : 0! = 1   (o fatorial de zero é igual a 1)   e que 1! = 1 ( o fatorial de 1 é igual a 1)

Combinação

Uma combinação sem repetição, em análise combinatória, indica quantas variedades de subconjuntos diferentes com n elementos existem em um conjunto U , com r elementos. Só é usada quando não há repetição de membros dentro do conjunto.

Na combinação simples, a ordem dos elementos no agrupamento não interfere. São arranjos que se diferenciam somente pela natureza de seus elementos.

Portanto, se temos um conjunto A formado por n elementos tomados p a p, qualquer subconjunto de A formado por p elementos será uma combinação, dada pela seguinte expressão:

(fonte: Brasil Escola)

Fatorial

Na matemática, o fatorial (AO 1945: factorial) de um número natural n, representado por n!, é o produto de todos os inteiros positivos menores ou iguais a n.

A notação n! foi introduzida por Christian Kramp em 1808.(Wikipédia)

Considerando n um número natural maior que 1 (um), podemos definir como fatorial desse número n (n!) o número:

n! = n(n – 1)(n – 2)(n – 3) * ...* 3 * 2 * 1

Lê-se n! como n fatorial ou fatorial de n.

Veja alguns exemplos de cálculos de fatorial de um número :

5! = 5 * 4 * 3 * 2 * 1 = 120
8! = 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 = 40320
6! = 6 * 5 * 4 * 3 * 2 * 1 = 720
10! = 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 = 3.628.800

Com isso creio que já deu para recordar o básico sobre Arranjo, Permutação, Combinação e Fatorial.

Vamos então ao que realmente interessa...

Como podemos fazer para implementar esses cálculos no Visual Basic ?

Fazendo Cálculos com o Visual Basic

A seguir temos um singelo programa feito na linguagem Visual Basic que permite calcular permutações, combinações e o fatorial de um número dado:

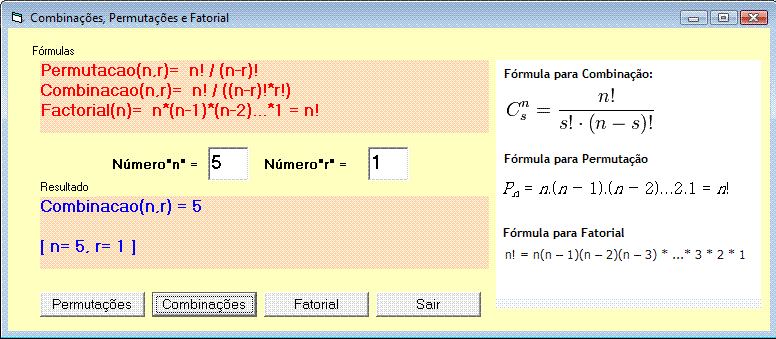O cálculo não esta otimizado e existe um valor máximo acima do qual poderá ocorrer um erro de overflow, mas você pode aperfeiçoar o algoritmo tornando-o mais rápido e calculando valores maiores.

Pegue os projetos completos aqui : CombinacaoVB.zip

Eu sei é apenas VB mas eu gosto...

"Meus filhinhos , estas coisas vos escrevo, para que não pequeis; e se alguém pecar, temos um advogado para com o Pai, Jesus Cristo, o justo." I João 2:1

Referências:

José Carlos Macoratti